Quantum numbers are numbers developed to specify the energies and general
behavior of electrons in an atom. They are of four types:
The Principal Quantum Number (n)
The principal quantum
number designates the shell or energy level in which an electron is (it is the same as Bohr’s quantum number, n). It has values from 1 up to infinity, i.e., n=1, 2, 3, 4,... It is the most important of the quantum numbers.
Angular Momentum or Azimuthal Quantum Number (
i )
The
angular momentum or Azimuthal quantum number designates the angular momentum of an electron. Due to its circular motion, an electron also possesses angular kinetic energy, which is reduced by the total energy of the electron. Since n determines the energy of the electron, the allowed
values of i must be restricted by the values of n.
Both theory and experiments show i
to have values 0, 1, 2,... (n-2), (n-1). Thus if n=1, the value of
i
=1-1=0 . When n=2, i
can have two possible values, i.e., 0 and 1; when n=3,
i
can have three possible values, i.e., 0, 1 and 2; and when n=4,
i
can have four possible values, i.e., 0, 1, 2 and 3, etc. The total number of
i
values given for a particular n gives the number of sub-energy levels (or sub-shells) present in the given shell, in which an electron of a particular
i value can be found.
For example,
K shell, n=1 contains only one sub-shell; L shell, n=2 contains two; M shell, n=3 contains three; and N shell, n=4 contains four sub-shells.
The value of i
quantum number specifies the area or region in space in which the probability of locating an electron is high. This area is called orbital.
Orbital
An orbital is the area or region within an atom, in which the possibility of locating an electron is high, say 95%, and which can be occupied by no more than two electrons.
When an electron has i value of zero, it
means it can be located in an area or region which is spherically symmetrical in shape. This region is known as the s orbital.
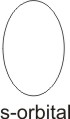
For
i value of 1, the electron
can be found in the p orbital,
which is dumb-bell in shape.
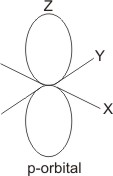
For
i values of 2 and 3, the electron is in the d (double dumb-bell in shape) and f orbitals respectively
Magnetic Quantum Number (m)
Magnetic
quantum number designates or specifies the observed magnetism which an electron creates. Since an electron possesses angular
momentum, then it can be thought of as an electric current circulating in a loop, thereby creating a magnetic field.
m values depend on
i value because the observed magnetism originates from angular
momentum. m has integral values varying from -
i to +
i .
When
i = 0, m = 0;
i = 1, m = -1, 0 and +1;
i = 2, m = - 2, -1, 0, +1 and +2; and when
i = 3,
m = -3, -2, -1, 0, +1, +2, and +3.
The value of m for an electron specifies its orientation or direction in space, due to its specific magnetism. The total number of m values obtained for a given
i value indicates the number of orientations which are possible for the given orbital. E.g., for
i = 0, there is 1 possible orientation of the s orbital;
i = 1, there are three possible orientations in space, giving rise to three p orbitals, which are close in energy and directed in space perpendicular to each other - these are the px, py and pz orbitals (also called degenerates).
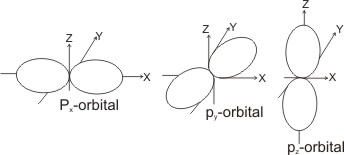
For
i = 2, there are five possible orientations of the d orbital, giving rise to five degenerate d orbitals.
For
i = 3, there are seven possible orientations of the f orbital, giving rise to seven degenerate f orbitals.
Spin Quantum Number (ms)
Spin
quantum number specifies the spin of an electron. An electron can spin about its own axis as it goes round the nucleus. It can spin clockwise or anticlockwise. If it spins in the same direction as the direction of its angular motion, it will make a slight contribution to the energy, but if it spins in opposite direction to the angular motion, there will be a slight reduction in the energy.
This effect, however small explains the double lines observed in many spectral lines. ms has only two possible values, +1/2 and -1/2 (representing clockwise and anticlockwise spins).
Note: Each electron in an atom is
described by a specific combination of the four quantum numbers.
For example, if there are two electron in the K shell, one of them can be described by n = 1,
i = 0, m = 0 and
ms = +1/2 , while the other can be described by n = 1,
i = 0, m = 0 and ms
= -1/2
Since the value of n restricts the value of
i and that of
i restricts that of m, only certain combinations of the quantum numbers will be allowed.
No two electrons in an atom have all the four quantum numbers alike. Even if they have the other three alike, they will differ in their spin quantum number. This is because, no two electrons can exist in the same orbital if they have the same spin - this is the Pauli’s Exclusion Principle.