Home

Gas Laws

To understand gas laws, you first need to understand the basic characteristics of gases. These include the following facts:

- Gases are easily compressible – i.e., in the gaseous state, matter is not compact.

- Gases exert pressure.

- Gases are highly expansible.

- Gases diffuse completely into one another, so that any mixture of gases is homogeneous.

Note: the parameters used in describing gases are volume; pressure and temperature. A change in the temperature or pressure will affect the volume.

Boyle’s law states that the volume of a given mass of a gas is inversely proportional to the pressure at constant temperature.

What the law is simply saying is that at constant temperature, doubly the pressure of a given mass of gas, the volume is decreased by half.

I.e. V α 1/P ;

V = k/P

PV = k (the product of P and V is a constant).

lf V₁ is the original or initial volume of the gas at pressure P₁, and V₂ the volume at a final pressure P₂, then

V₁ / V₂ = P₂ / P₁

or P₁V₁ = P₂V₂

Boyle’s law is illustrated by the P – V curve below:

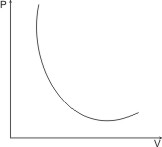
Note: Boyle’s law is not obeyed at low temperatures and high pressures (experiments show that PV Product is not constant at these conditions).

A flask is made of two vessels A (100 cm³ capacity) and B (300 cm³ capacity) separated by a tap. A was filled with a gas at 748 KNM^-2 pressure and B was evacuated until the pressure inside it was negligible. Assuming that the temperature remains constant, calculate the pressure in the flask when the tap is opened, allowing gas to flow from A to B.

Solution:

V₁/V₂ = P₂/P₁ Where V₁ = 100 cm³, V₂ = sum of volumes A and B = 400 cm³, P₁ = 748 KNM^-2, V₁ = ?

100/400 = P₂/748

P₂ = 748 x 100/400 = 187 KNM^-2

Note: The initial pressure is due only to the effect of gas A, thus initial volume is that of only A as well.

You don’t have to convert volume to m³, leave it in whatever unit it is given.

Charles’s law states that, at constant pressure, the volume of a fixed mass of gas is directly proportional to its absolute temperature. This means that if the temperature of a gas is doubled, its volume is doubled as well, and if the temperature is halved, its volume is also halved.

I.e., V α T ;

V = kT ;

k= V/T

If V₁ is the volume of a fixed mass of a gas at the absolute temperature T₁, and V₂ is volume at temperature T₂,

then: V₁/T_I = V₂/T₂ = k

The figure below illustrates Charles’ law.

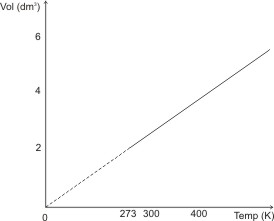
or

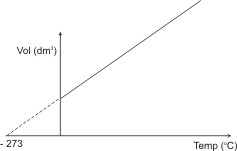
 If a gas were to follow the above relationship indefinitely upon cooling, its volume would be reduced to 0 (zero) at -273 ^oC (or 0 ^oK). Actually, all gases have been found to liquefy before this temperature is reached. This temperature is called the absolute zero.

It is the temperature (-273 ^oC or 0 ^oK) whereby theoretically, gases become liquid.

Note: Charles’ law, like Boyle’s law is not obeyed at low temperatures and high pressures - the observed volume is less than that predicted by Charles’ law.

Hence, both Charles’ and Boyle’s laws only apply to the behavior of an ideal or perfect gas.

A fixed mass of gas has a volume of 200 cm³ at 27^oC, calculate the volume when the temperature is increased to 87^oC and the pressure kept constant.

Solution:

V₁/T_I = V₂/T₂ Where V₁ = 200 cm³, V₂ = ?, T₁ = (273 + 27 = 300 K) , T₂ = (273 + 87 = 360 K)

200/300 = V₂/360

V₂ = 360 X 200 /300 = 2 X 120 = 240 cm³

A combination of Boyle’s and Charles’ laws gives the combined gas law.

I.e. P₁V₁/T₁ = P₂V₂/T₂ = k

This can be used to calculate the temperature, pressure or volume of a given mass of a gas under different conditions.

A given mass of a gas has a volume of 7.5 dm³ at 250 K and 80 K N M^-2. Calculate the pressure at which it will have a volume of 7.2 dm³ at 270 K.

Solution: P₁V₁/T₁ = P₂V₂/T₂

Where P₁ = 80 KNM^-2, P₂ = ?, V₁ = 7.5 dm³, V₂ = 7.2 dm³, T₁ = 250 K, T₂ = 270 K

80 X 7.5 / 250 = P₂ x 7.2 / 270

P₂ = 270 x 80 x 7.5 / 250 x 7.2 = 90 KNM^-2